くらしのマーケット開発ブログ

「くらしのマーケット」を運営する、みんなのマーケット株式会社のテックブログです

トップ > 凸最適化問題の紹介

凸最適化問題の紹介

はじめに

テックチームのトゥエンです。

この記事では、機械学習や他の多くの分野に適用される興味深い部分を紹介します。 それは凸最適化問題です。

f:id:curama-tech:20180820161856j:plain

問題

めぐみさんは、ワインが大好きです。ワインが大好きすぎて自分でワインを作ることにしました。 めぐみさんは、ワインを作るためのフルーツとして葡萄と苺を育て、ワインにすることにしました。 しかし、安く早くワインが飲みたいめぐみさんは予算は1万8千円、期間は1ヶ月（30日）でワインを作りたいと思っています。また、 めぐみさんは畑を所有しており、その畑の面積は800平方メートルあります。葡萄栽培のコストは3千円、苺は千円です。葡萄の栽培時間は、100平方メートルあたり2日間、苺の栽培時間は100平方メートルあたり5日間です。100平方メートルあたり葡萄は50リットルのワイン、100平方メートルあたり苺は30リットルのワインを作ることができます。 最も多くワインを栽培する方法を教えてください。

これを最適化問題と呼んでいます。今回は、最適化問題の中でも凸最適化問題という手法を使って問題を解いていきます。

上の問題を解決するのは簡単ですが、実際に起こる問題はもっと複雑です。

問題を解決する方法をより深く理解するために、数学的基礎について少し紹介したいと思います。

少し数学について

最適化問題

最適化問題（optimization problem）とは、特定の集合上で定義された実数値関数または整数値関数についてその値が最小（もしくは最大）となる状態を解析する問題です。

最適化問題の公式は、

f:id:curama-tech:20180822111115p:plain:w300

  • { \displaystyle f(x) }：目的関数
  • { \displaystyle g_i(x), h_j(x) }：制約条件

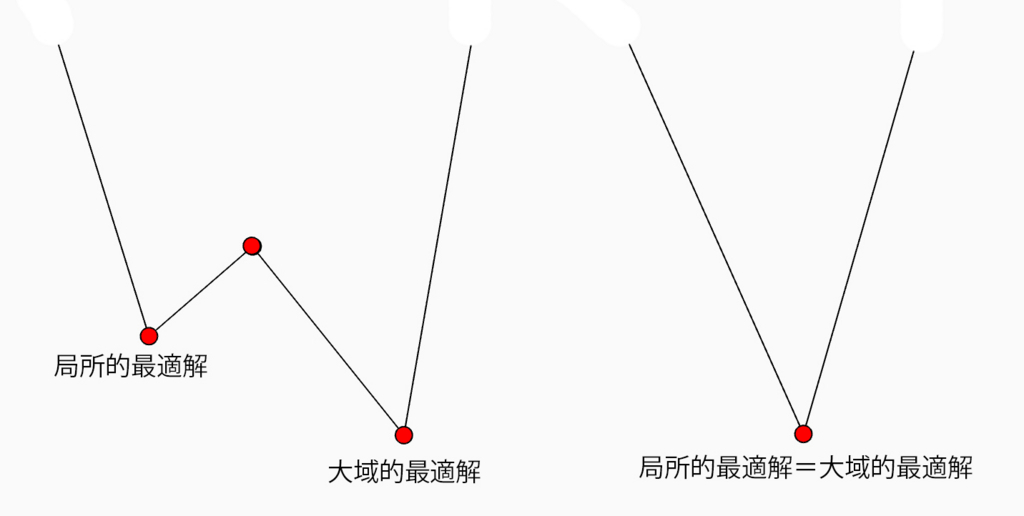
最適化問題では、大域的最適解 (globally optimal point) ではなく局所的最適解 (locally optimal point) だけが見つかる場合があります。それは、最高の解決策ではないかもしれません。

f:id:curama-tech:20180820161820p:plain

したがって、次のセクションでは、凸集合と凸最適化問題について議論し、その特殊な性質から、上記の問題を回避することができます。

凸集合

ユークリッド空間における物体が凸（convex）であるとは、その物体に含まれる任意の2点に対し、それら2点を結ぶ線分上の任意の点がまたその物体に含まれることを言います。

f:id:curama-tech:20180820161749p:plain

集合 { \displaystyle C } が凸であるとき、任意の { \displaystyle x, y \epsilon C } および任意の λ ∈ [0, 1] に対し、点 { \displaystyle \lambda x + (1-\lambda)y } もまた { \displaystyle C } に属することをいう。

凸最適化問題

凸最適化問題の公式は、

f:id:curama-tech:20180822111115p:plain:w300

ここで、

凸最適化問題では、局所的最適解（local optimal solution）は大域的最適解（global optimal solution）です。この性質は結果を確実にすることができる最善の選択肢です。

f:id:curama-tech:20180820161608j:plain

問題の例

このセクションでは、凸最適化問題について簡単な例を見ましょう！

デモのために、Pythonと CVXOPT ライブラリ を使います。

線型計画法

線型計画法の公式は、

f:id:curama-tech:20180822133336p:plain:w160

例

この記事の冒頭の例は、線形計画法を利用して問題を解きましょう。

数学の実装のために、 { \displaystyle x } は葡萄の面積、 { \displaystyle y } は苺の面積です。

  • ワインの量は { \displaystyle 50x+30y }。

  • 畑の面積は800平方メートルです。 { \displaystyle \Rightarrow x+y \leq 8 }

  • 葡萄栽培のコストは3千円、苺は千円、最大コストは1万8千円です。 { \displaystyle \Rightarrow 3x+y \leq 18 }

  • 葡萄の栽培時間は、100平方メートルあたり2日間、苺の栽培時間は100平方メートルあたり5日間です、最大で30日かかります。 { \displaystyle \Rightarrow 2x+5y \leq 30 }

問題は次のように表されます。

f:id:curama-tech:20180822134145p:plain:w200

デモ

上記の式は次のように書き直すことができます。

f:id:curama-tech:20180822134423p:plain:w200

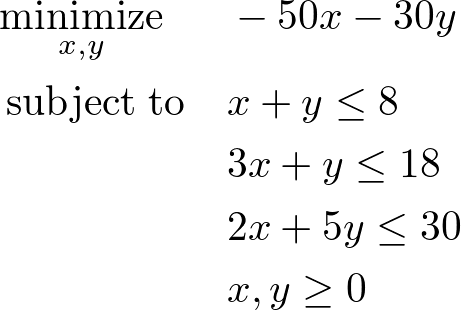
また、行列を使って上記の式を表すと以下のようになります。

f:id:curama-tech:20180822151538p:plain:w280

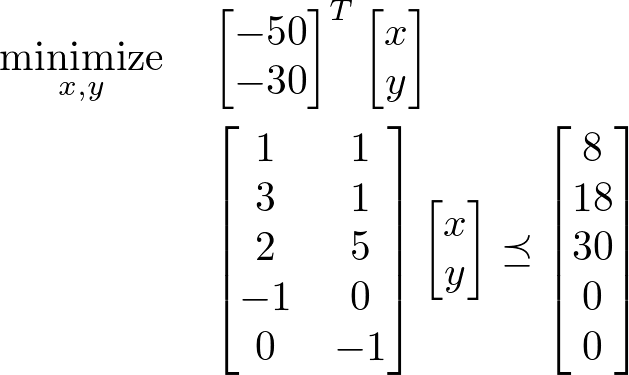
from cvxopt import matrix, solvers

c = matrix([-50., -30.])
G = matrix([[1., 3., 2., -1., 0.], 
            [1., 1., 5., 0., -1.]])
h = matrix([8., 18., 30., 0., 0.])

solvers.options['show_progress'] = False
sol = solvers.lp(c, G, h)

print(sol['x'])

結果

[ 5.00e+00]
[ 3.00e+00]

最適な解決策は、500平方メートルの葡萄と300平方メートルの苺を植えます。なので、めぐみさんは340リットルのワインを作ることができます。

二次計画法

次は、二次計画法問題という線形計画法問題の拡大を見てみましょう。この問題の公式は、

f:id:curama-tech:20180822134830p:plain:w240

{ \displaystyle P = 0 } なら線形計画問題になります。

例

次の問題を解きしましょう。

f:id:curama-tech:20180822135151p:plain:w270

デモ

上記の式は次のように書き直すことができます。

f:id:curama-tech:20180822152105p:plain:w420

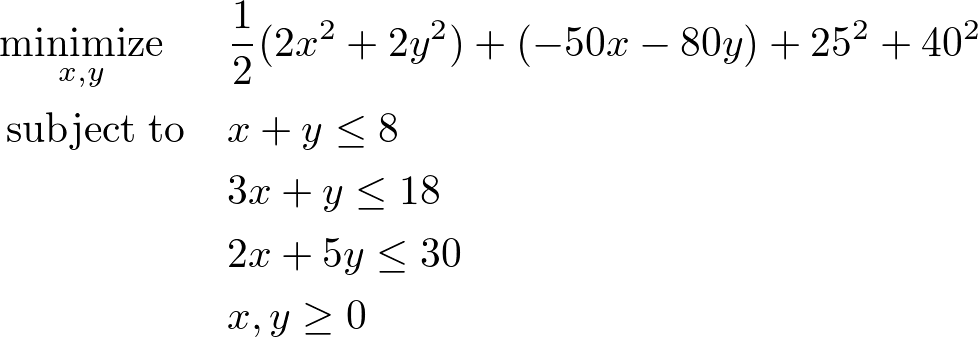
また、行列を使って上記の式を表すと以下のようになります。

f:id:curama-tech:20180822152629p:plain:w350

from cvxopt import matrix, solvers

P = matrix([[2., 0.], [0., 2.]])
q = matrix([-50., -80.])
G = matrix([[1., 3., 2., -1., 0.], 
            [1., 1., 5., 0., -1.]])
h = matrix([8., 18., 30., 0., 0.])

solvers.options['show_progress'] = False
sol = solvers.qp(P, q, G, h)

print(sol['x'])

結果

[ 3.33e+00]
[ 4.67e+00]

よって、 { \displaystyle x=10/3, y=14/3 } のとき、 { \displaystyle (x-25)^{2}+(y-40)^{2} } の値は最小です。

まとめ

  • 凸最適問題は非常に実用的な問題です。

  • このブログでは、凸最適化問題の2つの基本的な数学的モデル、線型計画法と二次計画法を紹介しました。

  • CVXOPTライブラリは、凸最適化問題を素早くきれいに解決するのに役立ちます。

あなたは多くの条件で問題を抱えたことがありますか？この記事がお役に立てば幸いです。

一緒に働いてみたいといった方もぜひお待ちしてます！ 次回は都築さんが書く予定です。

お読みになっていただきありがとうございます!

参考文献

[1] ウィキペディア

[2] Convex Optimization – Boyd and Vandenberghe, Cambridge University Press, 2004

[3] Machine Learning co ban - Vu Huu Tiep, 2018

[4] CVXOPT